机器学习3

学习率α 和 调试(Debugging)

保证梯度下降算法正常工作
梯度下降算法的作用是找到一个theta值来使代价函数J(theta)最小化.

在梯度下降算法执行时, 记录J(theta)的值, 以迭代次数为X轴, J(theta)的值为Y轴绘出图像. 如果梯度下降算法正常, 那么每次迭代J(theta)的值都会下降. 同时图像也可以让我们观察梯度下降算法是否已经收敛.

如果随着迭代次数的增加, J(theta)不断上升, 最常见的原因是:alpha的值太大, 应该减小alpha的值. 如果J(theta)的值不断震荡, 也应该减小alpha的值.

但是如果alpha太小, 梯度下降算法会下降得很慢.

多项式回归

如何将模型和数据进行拟合?
多项式回归: 用假设的一次项特征来代替高次项特征.

正规方程Normal eqution

正规方程提供了一种求theta的解析解法, 可以一次性求解theta的最优解.

当形如二次函数的J(theta)中的theta为实数时,最低点的导数=0, 利用这个条件就可以求解方程. 但是如果theta是一个向量, 那就需要对向量中的每一个特征值进行偏导=0的方程求解. 得到的每个theta的值组成的向量就是最小值.

有一个m=4的训练样本:

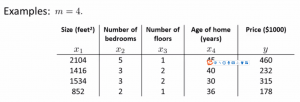
在第一列前补充一列x_0=1, 将x变成一个m*n+1的矩阵. 同时将y也变为一个m维向量. 在有m个训练样本(x^1,y^1),dots,(x^m,y^m) , n个特征值: x^i = {begin{bmatrix} x_0^i\x_1^i\ vdots x_n^i end{bmatrix}}的情况下. 可以得到使得代价函数最小化的theta为 :

theta=(X^TX)^{-1}X^Ty

使用正规方程不需要选择学习率alpha, 不需要进行迭代. 但梯度下降算法对于大数据量仍能保持正常工作. 而正规方程需要计算(X^TX)^{-1}, 在数据量较大时计算比较缓慢.

如果(X^TX)是一个不可逆的奇异矩阵. 一般来说, (X^TX)不可逆的原因是有多余的特征值(比如有两个特征值线性相关)或者特征值过多. 在Octave中, 使用pinv可以得到伪逆. 这样矩阵是一定能求出逆的(使用inv求出的是真实的逆).